Для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не менятеся. Иначе говоря, при любых натуральных значениях a, b и c верно равенство: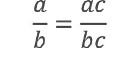

Докажем, что это равенство верно не только при натуральных, но и при любых других значениях a, b и c, при которых знаменатель отличен от 0, то есть при b ≠ 0, c ≠ 0.

Пусть a/b=m, тогда по определению частного a=b*m, умножим обе части этого равенства на c:

ac = (bm)c

На основании переместительного и сочетательного свойств умножения имеем:

ac = (bc)m

Так как bc ≠ 0, то по определению частного: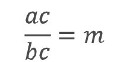

Значит: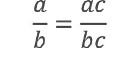

Итак, для любых значение a, b, c, где b ≠ 0, c ≠ 0 верно равенство: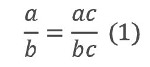

Тождества - равенства, верные при всех допустимых щначениях входящих в него переменных. Два выражения, принимающие равные значения при всех допустимых для них значениях переменных, называют тождественно равными выражениями, а замену одного такого выражения другим - тождественным преобразованием выражения.

Мы доказали, что равенство (1) верно при всех допустимых значениях переменных, значит это равенство является тождественным. Свойство выраженное тождеством: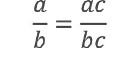

называется основным свойством дроби.

Поменяв в тождестве (1) левую и правую части получим выражение:

Данное тождество позволяет заменить дробь вида: ac/bc тождественно равной дробью: a/b. Или, как говорится, сократить дробь ac/bc на общий множитель c числителя и знаменателя.